I discovered a significant error in the simulations I ran in the previous post. So I'd like to present the corrected simulations, and also explain more deeply the assumptions and known weaknesses even in these fixed simulations. I also made the charts easier to use. However, I won't re-explain the background, so please see the previous post for that.

Summary for those who don't want to read the whole thing: Using an interval modifier near 140% is probably a reasonable default for language learning with Anki.

The Error(s)

The major mistake I made was failing to account for the additional reviews that you do after lapsing on a card. This, unsurprisingly, has a huge impact on the results. In fact, the amount of extra time you spend on a lapse has a far more significant impact than the initial time you spend creating and learning a new card.

I also had an error that Matt vs Japan caught in his own work, which is that calculating the total number of cards you know isn't quite as simple as just counting the cards in your deck. There's a forumla that the Supermemo people derived to get a correct approximation of known cards at any given point in time, and I am now using that. This also turns out to have a significant impact on the results.

Assumptions and Limitations

Before I jump into the updated results, I want to lay out more explicitly what the assumptions of my simulations are, as well as some limitations you should be aware of.

Anki Settings

I'll actually cover a few variations in the results, but the simulation's assumption about Anki settings is that you are pretty much using the defaults (aside from the Interval Modifier, of course).

The only exception is the lapse "new interval" setting, which determines how much a card's interval is reduced when you lapse on it. The Anki default is to reset the interval to zero, but that seems like a flagrantly bad choice to me: if you already successfully remembered it just one interval prior, there's no reason to drop you back to square one. Matt vs Japan uses 75% as his default, but that also seems not optimal. If your interval grows by, for example, 10x every time you get it right, then dropping it to 75% seems like it doesn't go far enough. Alternatively, if you're only growing by 1.1x, then 75% drops you back too far.

What I've come up with—and this is totally just hand-waving "this seems reasonable" territory—is to configure it so that lapsing twice will reverse a single success. So, for example, if getting a card right increases the interval 4x, then lapsing will halve the interval, because halving something twice results in 1/4 the size, reversing the 4x. For the curious, the way to calculate that is 1.0 / sqrt(N), where N is how much your interval is multiplied on success (4.0 in the example I just gave).

Other than that, it's all Anki defaults (except where noted in the variations). My reasoning for this is that it's not clear what effect all of the settings have on retention etc., so sticking to the defaults gives us some reasonable confidence that the formulas for the interval modifier will apply with some accuracy.

The Simulated User

There are two properties of the simulated user that affect the simulation:

• How much time they spend creating and learning a new card.
• How much time they spend per review.

However, for the graphs the only thing that actually matters is the ratio between these two items. Knowing their absolute magnitudes is unnecessary for calculating optimal efficiency, although it may still be interesting.

The assumption I've used is that creating a new card and doing the initial reviews to learn it take a combined time of 120 seconds (or two minutes). And each individual review after that takes 20 seconds. These seem like reasonable numbers to me. Moreover, except at bizarre extremes (e.g. new cards take almost no time) it doesn't appear that the ratio impacted the graphs significantly.

Length of the Simulation

For all the simulations in this post, I use a simulated time of 365 days (one year). Doing it for fewer days or more days does impact the results some, but basing things on one year seems reasonable to me. If your cards grow older than a year, it's not totally clear to me how much you're really getting out of them—at least in the context of language learning. And studying for significantly less than a year doesn't make sense for seriously learning a language.

General Limitations

I alluded to this earlier, but there are things that these simulations don't account for. The biggest one is that it's not at all clear how the following variables impact retention of cards:

• Increasing/decreasing the number of reviews for initial learning of new cards.
• Increasing/decreasing the number of additional reviews after lapses.
• Increasing/decreasing the lapse "new interval" setting.

I mean, it's pretty clear that increasing the first two and decreasing the latter will improve retention, but it's not at all clear how to quantify that, or create formulas for them (or at least I don't know). This is also a limitation of Matt vs Japan's work, and the simulator that he's now using.

Because of that, the retention impacts of these factors are completely unaccounted for in these simulations. This means that the particular choice used for one of these factors, even though it affects the simulation, does not affect it accurately. For example, you could set the lapse new-interval setting to 100000% (1000x multiplier), so that whenever you lapse a card it will launch its interval into the stratosphere. From the simulation's perspective, that's a massive increase in efficiency, because it assumes the retention rate for that card still stays the same. But that's obviously false in reality—in reality that setting would be roughly equivalent to deleting all lapsed cards from your deck.

That's why I'm generally trying to stick to Anki's defaults, or at least "reasonable" settings. And that also means that all results from not only my simulations, but also from Matt or anybody else, should be treated as fuzzy guides, not as an exact science. There's a lot that we're not accounting for, and it's not totally clear how that affects the simulations.

Results

So with that out of the way, here are the results. As in the last post, here's how to interpret the graphs:

• The vertical axis is the Interval Modifier setting in Anki.
• The horizontal axis is your personal retention rate at (roughly) default Anki settings.
• The white strip is 99+% optimal efficiency.
• The light gray strip is 95+% optimal efficiency.

"Efficiency" in this case means "cards learned per hour of time studying". And studying includes both reviews and time spent creating and learning new cards.

All of these graphs are normalized, and therefore don't reflect efficiency differences between different graphs. They are also normalized individually within each vertical slice of pixels, and therefore also don't reflect differences in efficiency between personal retention rates. The latter is intentional, as it makes it easy to e.g. find your personal retention rate and determine what interval modifier results in your personal optimal efficiency. See the previous post for more details.

The "Reasonable" Graph

I actually have quite a few graphs this time, but this is the one I think most people should use:

It represents precisely the settings and simulated user I described earlier, and I think is a reasonable graph to work from. In particular, it assumes:

• An average of two minutes spent creating + learning each new card.
• An average of 20 seconds per review.
• A single additional review per lapse.
• A "max lapse" setting of 8 (cards are suspended when they exceed 8 lapses).
• The 1.0 / sqrt(N) lapse new-interval setting I described earlier.

The main take-away is that an interval modifier of around 140% gets you 95% efficiency in almost the entire 75%-95% personal retention rate range. Which is pretty great! So I think this is probably a good default. But going up as high as 160% also seems quite reasonable. And if you have especially good retention, even as high as 200% might make sense.

But now that we have the "reasonable" graph out of the way, let's start playing with the settings!

Varying Max Lapses

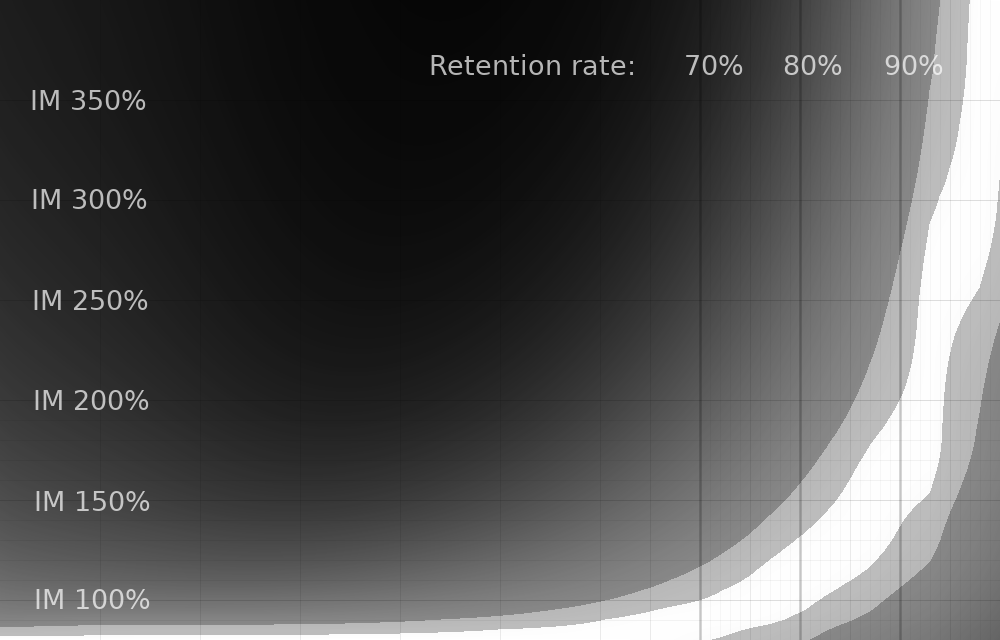
The above graph changes the "max lapse" setting to 4.

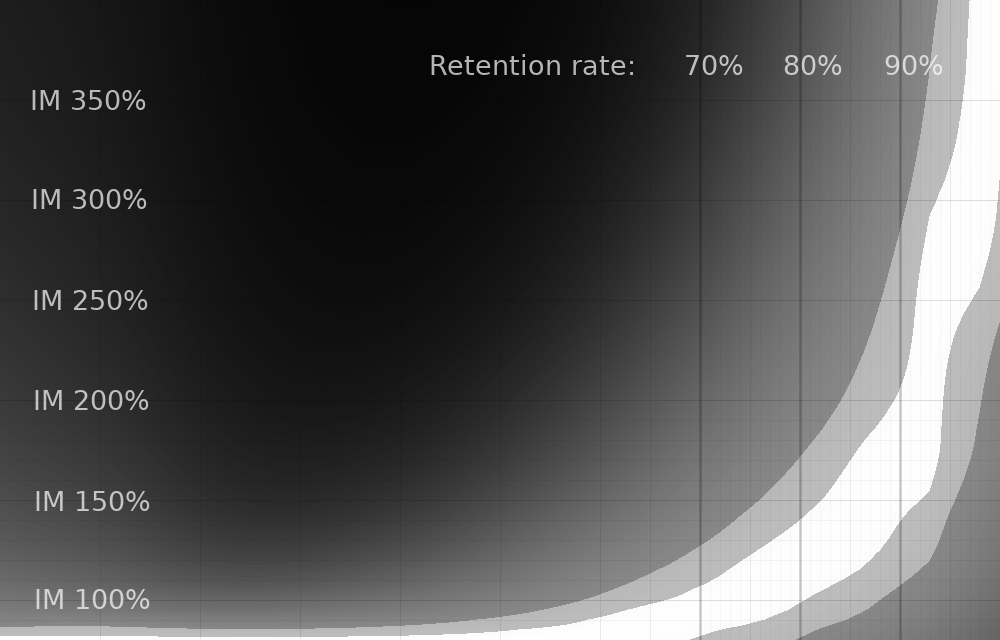
And this one changes the "max lapse" setting to 12.

These graphs together illustrate something useful: increasing your max lapse setting beyond 8 doesn't make much difference in efficiency, but lower numbers definitely do!

It's also worth noting (although not illustrated in the normalized graphs) that decreasing your max lapse setting has a negative impact on your efficiency. In general, with a max lapse setting of 8 or higher, you're at 99+% of optimal efficiency, but a setting of zero slashes your efficiency by a factor of 2, depending on your personal retention rate. A setting of 4 gives you 95+% max efficiency.

As far as the simulation is concerned, increasing your max lapse setting always improves efficiency. I think this makes sense. Although it's not in these simulations, I also did some sims where each card had a slightly different difficulty (i.e. individual retention rate), and the variance between cards had to get pretty huge before it wasn't always beneficial to increase max lapses.

So my takeaway is this: beyond a max lapse setting of 8 doesn't really make a difference to efficiency. But feel free to max out the setting if it makes you feel better.

However, there is also a psychological component to studying, and culling out cards you're having a tough time with might make sense. In that case, a setting of 4 probably makes sense, since it's pretty low but still has a minimal impact on efficiency.

Varying Additional Lapse Reviews

This should be taken with a significant grain of salt, as per the "limitations" section earlier in the article. But here are a few graphs varying how many additional reviews are done when you lapse. The "reasonable graph" earlier is "one additional review".

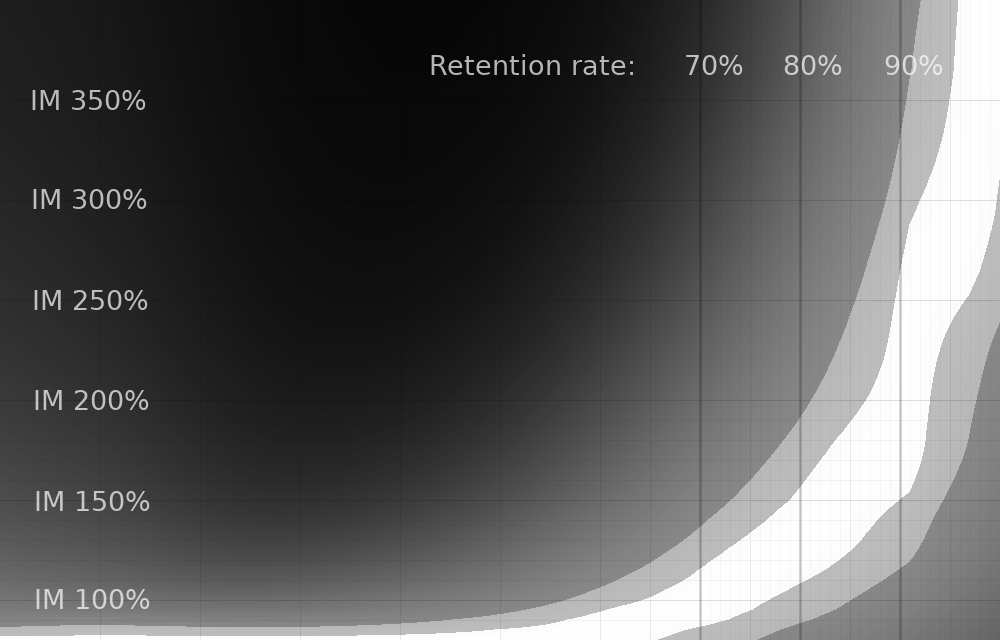
^ Zero additional reviews.

^ Two additional reviews.

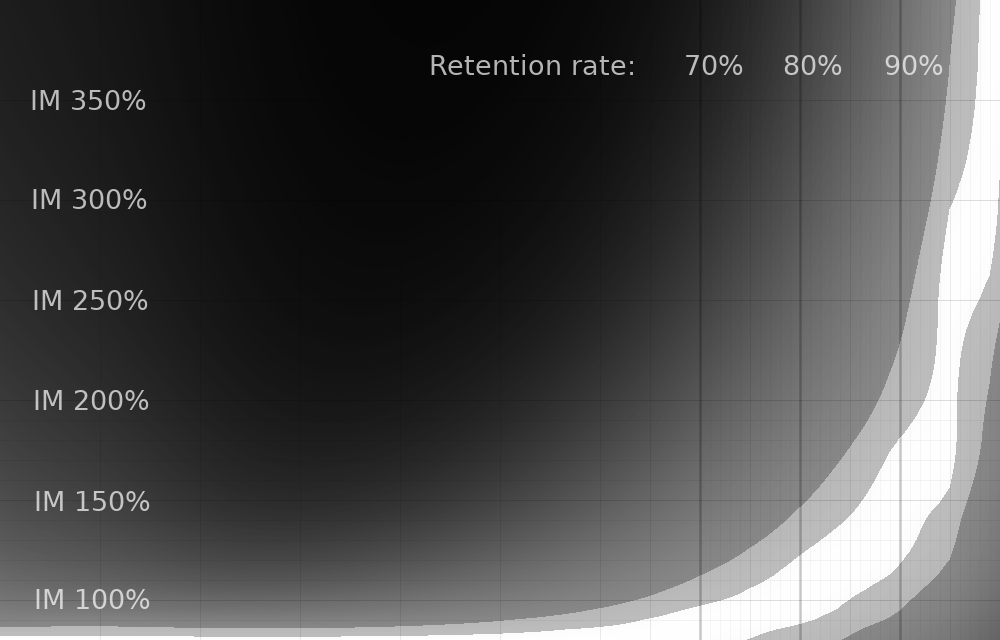
^ Three additional reviews.

The differences are pretty stark. Especially at zero additional reviews, it seems like you can get great efficiency with much larger interval modifiers! However, that seems very suspect to me, because the simulation isn't accounting for how these additional reviews may improve retention.

Having said that, because we don't know exactly how much those additional reviews help, any of these graphs are potentially as valid as the "reasonable" one that I presented. This is an open area for additional work. If anyone has any data about the impact of additional lapse reviews, I would be very interested to see it!

Varying Lapse New Interval

Finally, let's see how varying the lapse "new interval" setting (how much intervals are reduced on lapses) impacts things.

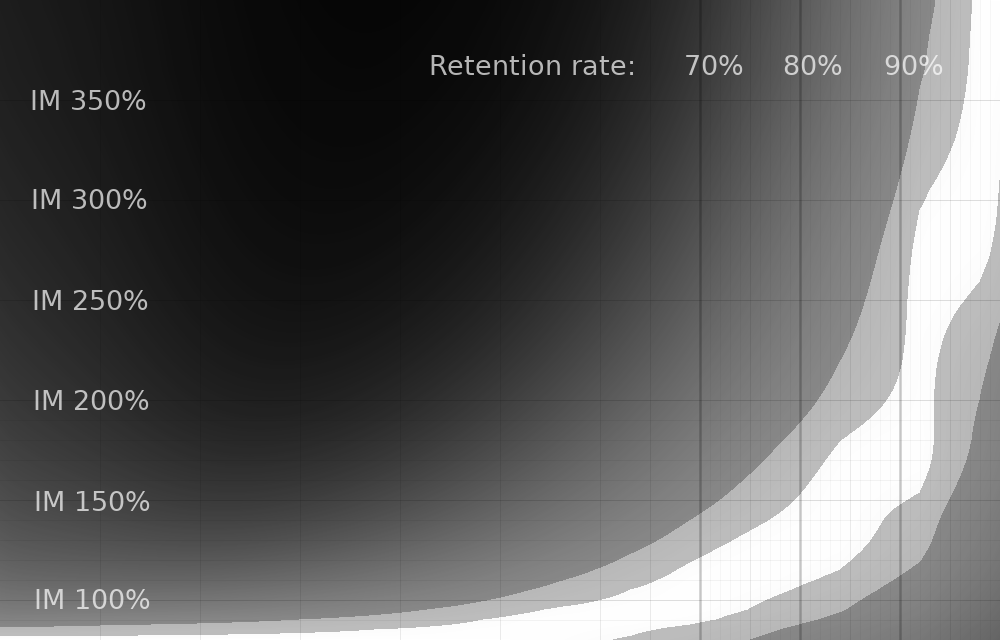
^ Matt's 75% setting.

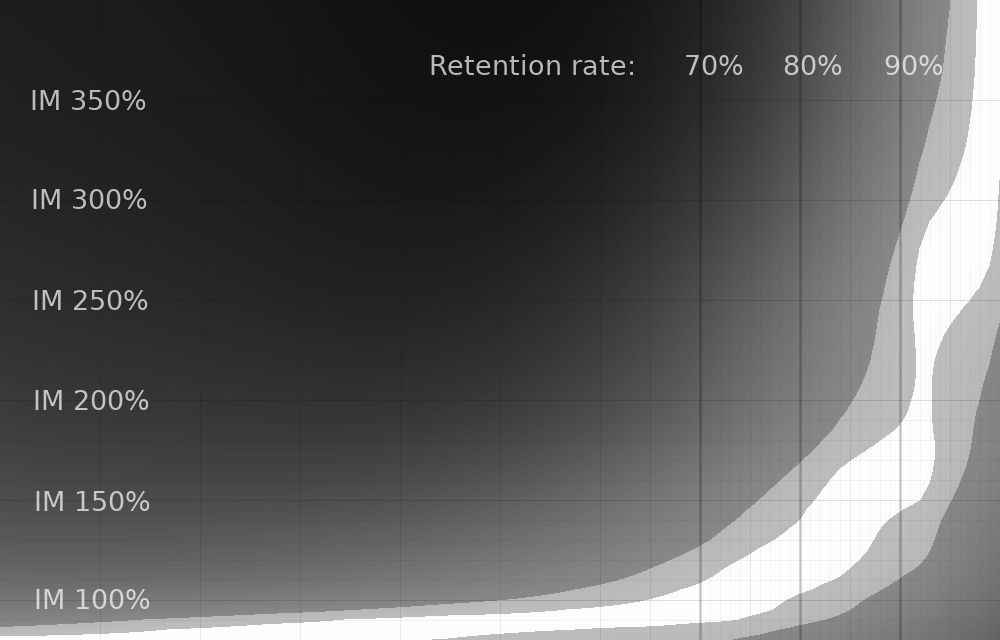
^ Anki's default 0% setting.

As you can see, this setting also has a notable impact. But just like varying the additional lapse reviews, I have no idea how this impacts things in reality—this simulation doesn't account for important (but currently unknown) factors. So this also needs further study!

Wrap-up

I'm reasonably confident in the results from these simulations, except for the limitations and unknown factors I've described throughout this post. If anyone has any insight around those issues, I would be very interested to hear from you!

But for now, I think it is at least reasonable to go with an interval modifier of %140. If you want to use my lapse "new interval" setting scheme, that corresponds to a lapse "new interval" settings of 53%.